Introduction
Set up
We are given the dataset \(X = \{ (\mathbf{x}_n, \mathbf{y}_n) \mid n=1,..,N \}\) that is a sequence of data points \((\mathbf{x}_n, \mathbf{y}_n) \in \mathbb{R}^{d_x} \times \mathbb{R}^{d_y}\), where \(N\) is the number of data points. \(\mathbf{x_n}\) are sampled from an unknown distribution \(\mathcal{D}\), and mapped to \(\mathbb{R}^{d_y}\) with an unknown function \(f(\mathbf{x_n}) = \mathbf{y_n}\), \(f\) determines the correct \(\mathbf{y}\) for each \(\mathbf{x}\).
Neural network
The neural nework is a parametric function \(NN: \mathbb{R}^{d_x} \to \mathbb{R}^{d_y}\) that tries to approximate the unknown \(f\): \[\hat{\mathbf{y}} = NN(\mathbf{x}, \Theta).\] \(\Theta\) is a vector of parameters. The neural network is composed of \(K\) layers (indexed with \(l=1,..,K\)) of simple functions \(g_l\) (neurons) whereby the output of a layer \(l\), \(\mathbf{o}_l\), plays the role of an input for the next layer \(l+1\). \(\Theta\) lumps together parameters of all layers (\(\mathbf{w}^l\) for all \(l\)).

\[\mathbf{o}^l = g_l(\mathbf{a}^l) = g_l(\mathbf{w}^l\mathbf{o}^{l-1})\] \[\mathbf{a}^l = \mathbf{w}^l\mathbf{o}^{l-1} = \mathbf{w}^lg_l(\mathbf{a}^{l-1})\]
where \(g_l\) is a nonlinear function, \(\mathbf{w}^l\) is \(N_l \times (N_{l-1}+1)\) matrix of parameters for the layer \(l\), \(N_l\) is the number of neurons in layer \(l\), \(\mathbf{o}^{l-1}\) is a \((N_{l-1}+1)\) column vector, \(\mathbf{a}^{l}\) is a \(N_{l}\) column vector. \(l=1,...,K\) is an index of the layer, \(K\) is the number of layers. The output of layer 0, corresponds to the input given to network, whereas the output of last K-th layer gives the output of the network: \(\hat{\mathbf{y}}_n \equiv \mathbf{o}^K\), \(\mathbf{o}^0 \equiv \mathbf{x}_n\).
Component-wise: \[a_i^l = \sum_{j=0}^{N_{l-1}} w_{ij}^l o_j^{l-1} = \sum_{j=1}^{N_{l-1}}w_{ij}^l o_j^{l-1} + b_i^l\]
where \(a_i^l\) is the activation of \(i\)-th neuron in layer \(l\), \(o_j^l\) is the output of \(j\)-th neuron, \(b_i^l = w_{i0}^l\) is bias (\(o_0^{l-1} \equiv 1\)), \(\Theta = \{ w_{ij}^l\ \mid \ \text{for all }i,j,l \}\).
We need to measure how bad is the approximation of \(f\) given by \(NN\). For this, we define the loss function \(L^{\text{true}}(\Theta)\): \[L^{\text{true}}(\Theta) = E_{\mathbf{x} \sim \mathcal{D}}[C(\hat{\mathbf{y}}(\mathbf{x}), f(\mathbf{x}))]\]
Ideally, the parameters of the network (\(\Theta\)) are chosen so that the loss is minimized:
\[\Theta^{*} = \mathrm{argmin}_{\Theta} L^{\text{true}}(\Theta)\]
Here \(C\) is the cost function that measures how bad \(NN\) performs for one point, e.g. \(C(\mathbf{z}, \mathbf{y})=\|\mathbf{z}-\mathbf{y}\|_2^2\).
In practice, having finite data set \(X\), we approximate expectation with average:
\[L^{\text{real}}(\Theta) \approx L(X, \Theta) = \frac{1}{N}\sum_{n=1}^{N}C(\hat{\mathbf{y}}(\mathbf{x}_n),\mathbf{y}_n)\]
To evaluate if this approximation was reasonable, we compute empirical loss \(L(X_{\text{test}}, \Theta)\) on another data set \(X_{\text{test}}\) and make sure that it is not too large compared to \(L(X, \Theta)\).
Searching for a good network
To minimize \(L\), gradient descent can be used, that is \(\Theta\) is updated according to:
\[\Theta_{t+1} = \Theta_t - \eta \nabla L(X, \Theta_t)\] Here \(t\) iteration of the algorithm, \(\eta\) is learning rate, \(\nabla\) denotes gradient operator.
The computation of the gradient is often done with a numerical version of automatic differentiation so-called backpropagation (it has nothing to do with backpropagation of action potential in Neuroscience).
Let’s derive components of \(\nabla L(X, \Theta_t)\) for a layer \(l\).
\[\frac{\partial L}{\partial w_{ij}^l} = \frac{1}{N} \sum_{n=1}^{N} \frac{\partial C(\hat{\mathbf{y}}(\mathbf{x}_n),\mathbf{y}_n)}{\partial w_{ij}^{l}}\] Or in vectorized form:
\[\mathbf{J}_L^l = \frac{1}{N}\sum_{n=1}^N \mathbf{J}_C^l(\hat{\mathbf{y}}(\mathbf{x}_n),\mathbf{y}_n)\]
Cost function \(C\) depends on \(\hat{\mathbf{y}}\), whereas each \(\hat{\mathbf{y}}\) (or output of the last layer) depends on outputs of previous layers \(\mathbf{o}^{l'}\) \(l`<K\), whereas parameters corresponding to layer \(l\) first appear in \(\mathbf{o}^l\):
\(C = C\left(\hat{\mathbf{y}}\left(\mathbf{o}^K(\mathbf{o}^l), \mathbf{o}^{K-1}(\mathbf{o}^l),...,\mathbf{o}^l\right)\right)\) and \(\mathbf{o}^l = \mathbf{o}^l(\mathbf{w}^l)\).
We can thus write:
\[\frac{\partial C}{\partial w_{ij}^l} = \frac{\partial C}{\partial a_i^l} \frac{\partial a_i^l}{\partial w_{ij}^l} = \frac{\partial C}{\partial o_i^l} \frac{\partial o_i^l}{\partial a_i^l} \frac{\partial a_i^l}{\partial w_{ij}^l} = \frac{\partial C}{\partial o_i^l} g_l'(a_i^l) o_j^{l-1} = \delta_i^l o_j^{l-1} \]
We can define Jacobian for \(C\) for each layer (\(J_{ij}^l = \frac{\partial C}{\partial w_{ij}^l}\)) and rewrite this equation in vectorized form:
\[\mathbf{J}^l = (\mathbf{\delta}^l) (\mathbf{o}^{l-1})^T\]
Here \(\delta_i^l = \frac{\partial C}{\partial a_i^l}\). In this formula, we can easily compute all except \(\frac{\partial C}{\partial o_i^l}\). However, for the last layer \(l=K\), as \(o_i^K = \hat{y}_i\), we can compute: \[\frac{\partial C}{\partial w_{ij}^K} = \frac{\partial C(\hat{\mathbf{y}}(\mathbf{x}),\mathbf{y})}{\partial \hat{y}_i} g_K'(a_i^K) o_j^{K-1},\]
which in vectorized form would be:
\[\mathbf{J}^K = (\nabla_{\hat{y}}C \odot g_K'(\mathbf{a}^K)) (\mathbf{o}^{K-1})^T.\]
If we know \(\frac{\partial C}{\partial o_i^l}\) and we can express \(\frac{\partial C}{\partial o_j^{l-1}}\) as a function of \(\frac{\partial C}{\partial o_i^l}\). After this, we will be able to compute \(\frac{\partial C}{\partial w_{ij}^{l-1}}\). As we already know \(\frac{\partial C}{\partial w_{ij}^{l}} = \frac{\partial C(\hat{\mathbf{y}}(\mathbf{x}_n),\mathbf{y}_n)}{\partial \hat{y}_i}\), we can recursively compute all components of \(\nabla_{\Theta} C\) going backwards in layers.
Let’s find \(\frac{\partial C}{\partial o_{j}^{l-1}} \mapsto \frac{\partial C}{\partial o_{i}^{l}}\).
\[C = C(\mathbf{o}^l(\mathbf{o}^{l-1}))\]
\[\frac{\partial C}{\partial o_{j}^{l-1}} = \sum_{i=0}^{N_l} \frac{\partial C}{\partial o_{i}^{l}} \frac{\partial o_i^{l}}{\partial o_{j}^{l-1}} = \sum_{i=0}^{N_l} \frac{\partial C}{\partial o_{i}^{l}} g_l'(a_i^l) w_{ij}^l = \sum_{i=0}^{N_l} \delta_i^l w_{ij}^l\]
We can rewrite in terms of \(\delta_i^l\):
\[\delta_j^{l-1} = \frac{\partial C}{\partial o_{j}^{l-1}} g_{l-1}'(a_j^{l-1}) = \left(\sum_{i=0}^{N_l} \delta_i^l w_{ij}^l\right) g_{l-1}'(a_j^{l-1})\]
In vectorized form:
\[\mathbf{\delta}^{l-1} = \left( (\mathbf{w}^l)^T \mathbf{\delta}^l \right) \odot g_{l-1}'(\mathbf{a}^{l-1})\]
Here \(\odot\) is elementwise product.
Algorithm
Forward pass for \((\mathbf{x}, \mathbf{y}) \in X\) to compute activations and outputs:
- Set \(\mathbf{o}^0 = \mathbf{x}\)
- For \(l=1,...,K\):
- \(\mathbf{a}^l = \mathbf{w}^l\mathbf{o}^{l-1}\)
- \(\mathbf{o}^l = g_l(\mathbf{a}^{l})\)
Backpropagation to compute gradient of the loss function:
- Take \(A \subseteq X\)
- For each \((\mathbf{x}_n, \mathbf{y}_n) \in A\):
- do forward pass to compute all \(g_l(\mathbf{a}^l)\)
- compute \(\mathbf{\delta^K} = \nabla_{\hat{y}}C \odot g_K'(\mathbf{a}^K)\)
- compute \(\mathbf{J}^K = (\mathbf{\delta}^K) (\mathbf{o}^{K-1})^T\)
- For \(l=K,K-1,...,2\)
- \(\mathbf{\delta}^{l-1} = \left( (\mathbf{w}^l)^T \mathbf{\delta}^l \right) \odot g_{l-1}'(\mathbf{a}^{l-1})\)
- compute \(\mathbf{J}^{l-1} = (\mathbf{\delta}^{l-1}) (\mathbf{o}^{l-2})^T\)
- Compute \(\mathbf{J}_L^l = \frac{1}{|A|}\sum_{n=1}^{|A|} \mathbf{J}_C^l(\hat{\mathbf{y}}(\mathbf{x}_n),\mathbf{y}_n)\) for all \(l\)
Stochastic gradient descent:
- For \(t=1,...,T\) do
- Select randomly \(A \subset X\)
- Do backpropagation for \(A\) to compute gradient \(\mathbf{J}_L^l\)
- For each \(l=1,...,K\) do
- \(\mathbf{w}^l_t = \mathbf{w}^l_{t-1} - \eta \mathbf{J}_L^l\)
Getting hands dirty with python and NumPy
First, I defined some useful general functions.
```python
import numpy as np
from copy import deepcopy
from functools import partial
import matplotlib.pyplot as plt
def sigmoid(x, derivative=False):
s = 1.0 / (1.0 + np.exp(-x))
if derivative:
return s * (1.0 - s)
else:
return s
sigmoid.name = 'sigmoid'
def updated(d, dupdate):
d = deepcopy(d)
d.update(dupdate)
return d
def shuffled(x):
x = deepcopy(x)
np.random.shuffle(x)
return x
def dataToBatches(data, batch_size):
lenData = len(data)
ilast = lenData // batch_size
start = 0
while start < lenData-1:
stop = min(lenData, start + batch_size)
yield data[start:stop]
start += batch_size
def grad_l2_cost(y, target):
return (target-y)
def l2_cost(nn, datapoint):
image, label_one_hot = datapoint
return np.mean((nn.forward(image)-label_one_hot)**2)
def lossData(nn, data):
return np.mean(list(map(partial(l2_cost, nn), data)))
def accuracy(nn, data):
return np.mean(
[ np.argmax(nn.forward(d[0])) == np.argmax(d[1])
for d in data
])
def one_hot_mnist(label):
x = np.zeros(10)
x[label] = 1.0
return x
```
Let’s define neural network class.
```python
class Layer():
def __init__(self, parameters):
self.W = parameters['init_weights'](
parameters['n_out'],
parameters['n_in'])
self.b = parameters['init_biases'](
parameters['n_out'])
self.Wb = np.hstack([self.b[:, np.newaxis], self.W])
self.act_func = parameters['act_func']
self.dact_func = parameters['dact_func']
self.dactivation = None # to keep track of its activation
self.output = None
def forward(self, inp):
inp = np.insert(inp, 0, 1.0)
activation = np.matmul(self.Wb, inp)
self.dactivation = self.dact_func(activation)
output = self.act_func(activation)
self.output = np.insert(output, 0, 1)
return output
def setLast(self):
for attr in ['output']:
setattr(self,
attr,
getattr(self, attr)[:-1])
def __repr__(self):
return "(Input, Output) size: {}".format(self.W.shape[::-1]) + "\n" +\
"Activation: {}".format(self.act_func.name) + "\n"
class Network():
def __init__(self, layers_pars, grad_cost):
self.layers = [Layer(par) for par in layers_pars]
self.grad_cost = grad_cost
def forward(self, inp):
out = inp
for l in self.layers:
out = l.forward(out)
l.setLast()
return out
def __repr__(self):
desc = ''
for i, l in enumerate(self.layers):
desc += "Layer {}\n".format(i)
desc += repr(l) + "\n"
return desc
def describe(self):
print(repr(self))
def gradient(self, data):
sum_Jls = np.zeros(len(self.layers))
lenData = 0
for x, y in data:
lenData += 1
output = self.forward(x)
delta = self.grad_cost(y, output)\
* self.layers[-1].dactivation
delta = delta[:, np.newaxis]
Jl = np.matmul(delta,
self.layers[-2].output[np.newaxis, :])
Jls = [Jl]
for l in range(len(self.layers)-1, 0, -1):
q1 = np.matmul(self.layers[l].Wb.T, delta)
q2 = self.layers[l-1].dactivation[:, np.newaxis]
delta = q1[1:] * q2
outprev = \
self.layers[l-2].output[np.newaxis, :]\
if l-2 > -1 else\
np.insert(x, 0, 1)[np.newaxis]
Jl = np.matmul(delta, outprev)
Jls.append(Jl)
sum_Jls = [ old+Jl for old,Jl in zip(sum_Jls, Jls) ]
mean_Jls = [ old / lenData for old in sum_Jls ]
# correct for reversion as a result of backward computation
mean_Jls = mean_Jls[::-1]
return mean_Jls
def SGD(self, data,
batch_size=100,
max_iter=None,
learning_rate=0.01):
if max_iter is None:
max_iter = len(data)
dataS = shuffled(data)
for i, batch in enumerate(
dataToBatches(dataS,
batch_size=batch_size)):
if i > max_iter:
break
Jls = self.gradient(batch)
for l in range(len(self.layers)):
self.layers[l].Wb -= learning_rate * Jls[l]
```
Let’s make a simple network where \(g_l(x) = 1/(1+e^{-x})\) is the same for all layers, load MNIST data and train network to classify digits.
```python
def mkSimpleNetwork(ns_per_layer):
parameters =\
{ 'init_weights': np.random.randn
, 'init_biases' : np.random.randn
, 'act_func' : sigmoid
, 'dact_func' : partial(sigmoid, derivative=True)
}
layers_pars = []
for n_in, n_out in zip(ns_per_layer[:-1],
ns_per_layer[1:]):
layers_pars.append(
updated(parameters,
{ 'n_in' : n_in
, 'n_out' : n_out
}))
return Network(layers_pars, grad_l2_cost)
def getData(
mnist_tuple,
subset=30000,
shuffle=True
):
images, labels = mnist_tuple
# Sequence X
data = list(
zip(images,
list(map(one_hot_mnist, labels))))
if shuffle:
data = shuffled(data)
if subset:
data = data[:subset]
return data
def scaleData(data, scaler=lambda x: np.array(x)/255.0):
return [(scaler(img), lbl) for img, lbl in data]
# helpers that are needed later on (skip them for now).
def extend_Wbls(nn, Wbls):
for i, l in enumerate(nn.layers):
Wbls[i] = np.vstack([Wbls[i], l.Wb.flatten()])
def plot_save(nn, loss, accs, Wbls, fpath='nnTrain.png'):
fig, axs = plt.subplots(
2+len(nn.layers), 1,
figsize=(6, 6))
for k in loss.keys():
axs[0].semilogy(loss[k], label=k)
axs[1].plot(accs[k], label=k)
axs[0].set_ylabel('loss')
axs[0].legend()
axs[1].set_ylabel('accuracy')
axs[1].legend()
for i in range(len(nn.layers)):
ax = axs[2+i]
c = ax.pcolor(Wbls[i].T, cmap='RdBu_r')
ax.set_ylabel("$\mathbf{w}^%i$" % (i+1))
fig.colorbar(c, ax=ax)
plt.tight_layout()
fig.savefig(fpath)
plt.close()
if __name__ == '__main__':
# Load and preprocess MNIST data
from mnist import MNIST
mndata = MNIST('/home/ilya/Downloads/MNIST/')
d = {}
d['train'] = scaleData(getData(
mndata.load_training()))
d['test'] = scaleData(getData(
mndata.load_testing()))
# Create simple network with two layers
nn = mkSimpleNetwork([784, 50, 10])
# initialize measurables
loss = {k:[lossData(nn, v)] for k, v in d.items()}
accs = {k:[accuracy(nn, v)] for k, v in d.items()}
Wbls = [l.Wb.flatten() for l in nn.layers]
# training loop
for n_epoch in range(30):
nn.SGD(d['train'],
max_iter=None,
batch_size=8,
learning_rate=3.0)
# compute measures and plot results
for k in d.keys():
loss[k].append(lossData(nn, d[k]))
accs[k].append(accuracy(nn, d[k]))
extend_Wbls(nn, Wbls)
plot_save(nn, loss, accs, Wbls)
print("Epoch {}: loss: {} acc: {}".format(
n_epoch,
loss['test'][-1],
accs['test'][-1]))
```
Results
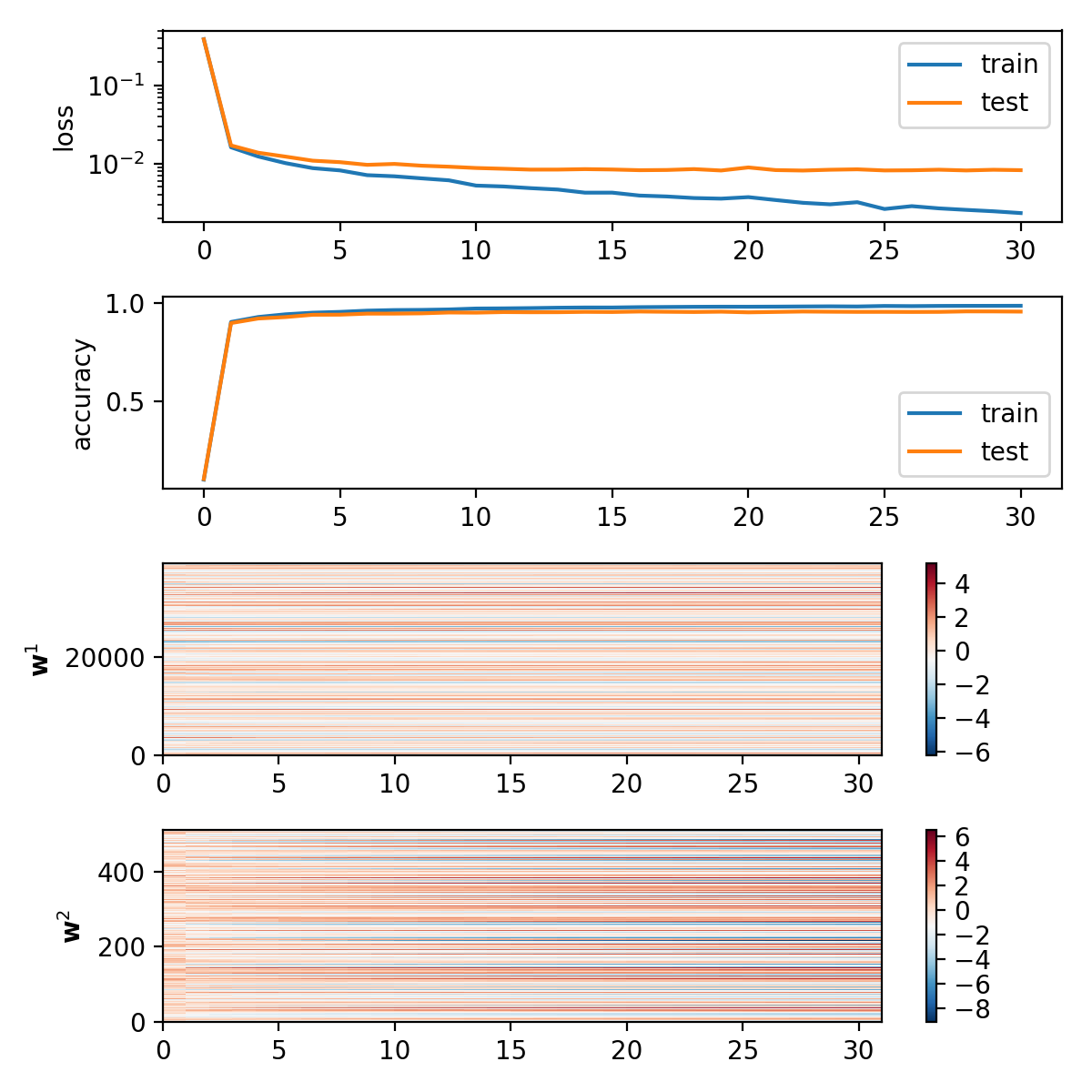
Epoch 0: loss: 0.016991653848590874 acc: 0.8966
Epoch 1: loss: 0.013715554862541645 acc: 0.9196
Epoch 2: loss: 0.012228999662532923 acc: 0.9269
Epoch 3: loss: 0.010847338415188106 acc: 0.9385
Epoch 4: loss: 0.01038737127915931 acc: 0.939
Epoch 5: loss: 0.009598660621545196 acc: 0.9442
Epoch 6: loss: 0.009858286550737687 acc: 0.9443
Epoch 7: loss: 0.009359748620839778 acc: 0.9457
Epoch 8: loss: 0.009088295631916992 acc: 0.95
Epoch 9: loss: 0.008745593652667713 acc: 0.9492
Epoch 10: loss: 0.008550893034509434 acc: 0.9521
Epoch 11: loss: 0.008339602288365305 acc: 0.9513
Epoch 12: loss: 0.00834561132452328 acc: 0.9515
Epoch 13: loss: 0.008456136266077822 acc: 0.9532
Epoch 14: loss: 0.008365949090187232 acc: 0.9525
Epoch 15: loss: 0.008197821605744322 acc: 0.9549
Epoch 16: loss: 0.008246864203031709 acc: 0.9536
Epoch 17: loss: 0.008465551030755258 acc: 0.9525
Epoch 18: loss: 0.008124560552781017 acc: 0.9541
Epoch 19: loss: 0.008889806361243542 acc: 0.9508
Epoch 20: loss: 0.008222358936366456 acc: 0.9528
Epoch 21: loss: 0.008115327748820329 acc: 0.9549
Epoch 22: loss: 0.008307595954575276 acc: 0.9539
Epoch 23: loss: 0.008410497112609237 acc: 0.9531
Epoch 24: loss: 0.008138048542561003 acc: 0.9532
Epoch 25: loss: 0.008175355271420938 acc: 0.9527
Epoch 26: loss: 0.008317691955677251 acc: 0.9531
Epoch 27: loss: 0.008137449156834158 acc: 0.9556
Epoch 28: loss: 0.008301935092177169 acc: 0.9554
Epoch 29: loss: 0.008204441135138874 acc: 0.9545